カオス理論が常識を覆す～バブルは再発し、野生動物は激減する、難解なカオス理論を易しく解説～

金融工学の理論上、バブルは起きないことになっています。ではなぜ起きないはずのバブルが起きるのでしょうか？
あるいは、近年のカツオやサンマの不漁が話題になっていますが、これは中国など他国の乱獲が原因なのでしょうか？
私たちの身近に起きる問題について、様々な原因が報道されています。

しかし、問題を解明する理論の前提が違っていたら、どうなるのでしょうか？

例えば、かつては地球を中心として太陽や惑星が回っていると考えられていました(天動説)。しかし天動説では惑星の動きを正確に表すことができませんでした。

そして現在は地球が太陽の周りを回っている地動説に置き換わりました。

同様に私たちの身近にある様々な現象は、天動説のような古い考え方で捉えようとしているのかもしれません。
 

1960年代に生まれ、1990年代以降注目されている「カオス理論」があります。

カオス理論では経済や自然現象に対し、それまで正しいとされてきた前提条件が違っていることが分かってきました。

カオス理論に照らすと世界はどのように見えるのでしょうか。
 

近代科学の成立と無視された世界

17世紀以前、世界は神話に支配されていました。
様々な物理現象は神によるものでした。

しかし17世紀にはいるとニュートンをはじめとする多くの科学者が様々な原理や法則を発見し、近代科学は大きく進歩しました。
こうして世界は神による神秘的なものから、様々な理論や数式で表すことができる時計仕掛けの世界に変わったのです。
 

時計仕掛けの世界観と自然界への応用

ニュートンの功績は、物理上の様々な運動法則を解き明かしたことと、微分・積分を確立したことです。
これにより物体の衝突から振り子の振動、天体の動きを数式で表すことができるようになりました。つまり様々な物理現象の結果が計算できるようになったのです。

20世紀にアインシュタインが相対性理論を確立するまで、ニュートンの物理学が唯一でした。今でもほとんどの物理現象はニュートンの理論で解くことができます。今の高校生や大学生が勉強しているのもニュートンの理論なのです。

このニュートンの理論は、それまでの神話から始まる神秘に満ちた世界観を、神秘性の全くない時計仕掛けの世界に変えました。
 

そしてニュートン(とライプニッツら)の打ち立てた微分・積分は、天体の運動以外にも様々な物理現象を微分方程式と数式で表すことを可能にしました。こうしてニュートンが開いた科学の扉から、多くの科学者が様々な自然現象に微分・積分を応用しました。

イギリスの数学者ブルック・テイラーは、微分方程式を使って振動が正弦波であることを発見しました。さらにフランスの数学者ジャン・ル・ロン・ダランベールは2つ以上の変数の現象を解く偏微分方程式を考えました。そしてこれを使って2つ以上の振動の重なりを解きました。
 

ジョゼフ・ルイ・ラグランジュはこの振動理論を音響学に発展させ、レオンハルト・オイラーはニュートンの理論を応用して水などの液体(流体)の流れを解き明かしました。(二人は18世紀最大の数学者と呼ばれています。)

ジョゼフ・フーリエは熱の流れに微分方程式を応用しました。ピエール・シモン・ド・ラプラスやシメオン・ドゥニ・ポアソンは、構造物(弾性体)の変形を解き明かしました。

こうした科学者の自然現象に対する解析と理解は急速に深まり、それを元に蒸気機関、発電所、モーターなどの技術は急速に進歩し、産業は大いに発展しました。
 

無視された世界

一方様々な物理現象を微分方程式で表すことができても、そこからその現象の結果を定量的に把握するには、その微分方程式を解いて数値解を出さなければなりません。
物理現象を微分方程式で表すことと、その微分方程式を解くことは別なのです。
例えば、微分方程式とは以下の式です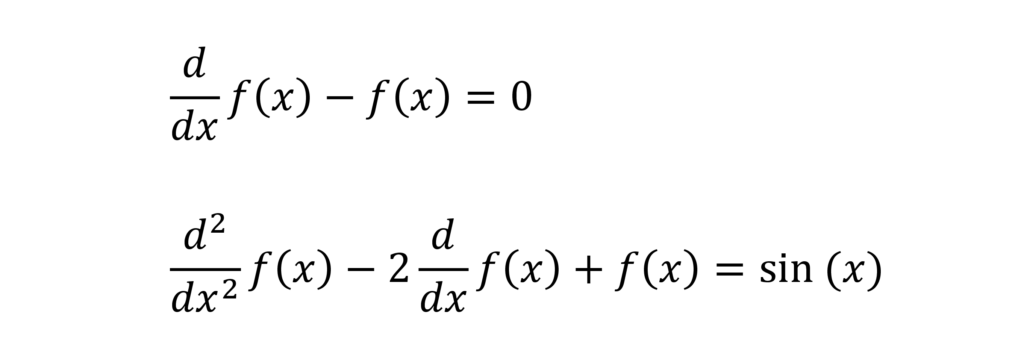

当時、微分方程式を解いて数値解を出すには、この微分方程式を展開して(解析的に)解かなければなりませんでした。これは今でも工学部の学生が試験でやっていることです。
一方、今では解析的に解かなくても、コンピューターを使って微分方程式の数値解を計算することができます。
 

しかし当時、例え自然現象を微分方程式で表すことができても、その微分方程式が複雑で解析的に解けなければ、その理論は現実には使えませんでした。そこでこのような場合、解析的に解けるように微分方程式の前提条件を変えました。

例えば物体の衝突を計算する場合、衝突する物体は

• 弾性変形や塑性変形が一切ない完全な剛体で
• 衝突の際に摩擦の影響も全くない

という条件です。
 

従ってパチンコ玉のような硬い物体が衝突した後の軌跡は、ニュートン力学では高い精度で計算できます。(それでも弾性変形が皆無ではないため誤差は生じます。) しかし車と車が衝突した場合、衝突後の2台の運動はニュートン力学では解けません。

また物体の衝突自体も物体が2つの場合はニュートン力学で計算できますが、3つ以上の場合は計算できません。

 

天体のような互いに引力が作用する場合も同様で、これは「三体問題」として現在でも物理学の大きなテーマとなっています。
 

また当時は微分方程式を解析的に解くには、微分方程式が「線形」である必要がありました。微分方程式の線形と非線形の違いは以下のようなものです。

微分方程式が線形であれば、解はひとつだけ存在します。これに対して非線形微分方程式では、解が存在するかどうか、また解が存在してもその解が一つかどうかわかりません。

そこで当時の科学者は、自然現象を少々無理をしてでも線形微分方程式で表しました。しかし実際は自然界の現象の多くは、正確に表すためには非線形微分方程式が必要でした。
 

注記)　微分方程式の数値解
多くの数学者が微分方程式の解法を探求しましたが、手計算で解析的に解ける微分方程式は限界がありました。そこでコンピューターを使って数値解を求める方法が研究され、コンピューターの進歩と共に発展しました。数値解を求める方法にはルンゲ・クッタ法、線形多段法、オイラー法などがあり、今でも多くの解法が研究されています。この方法であれば非線形微分方程式も数値解が得られます。
 

確率論とランダムさとは？

実は天体の運動は軌跡が一つしかありません。そのためニュートン力学で表すことができます。
では常に起きるとは限らないような物理現象は、どうやって数学で表すのでしょうか。
 

確率論の確立

決まって起きるとは限らない現象、その代表がルーレットやサイコロ、つまりギャンブルです。
このギャンブルを16世紀から17世紀にかけてカルダーノ、パスカル、フェルマー、ホイヘンスらが数学の一分野として研究しました。

そして、その結果「確率論」が生まれました。
 

イタリアの数学者カルダーノは、賭博師でもありました。彼は1560年代『さいころあそびについて』で初めて確率論を系統的に論じました。

ラプラスは1814年に『確率の哲学的試論』でそれまでの様々な確率論を統合し、古典的確率論にまとめました。さらにベルヌーイは完全にバランスの取れたコインを投げた場合、回数が多くなれば表と裏の確率が半々になることを「大数の法則」で証明しました。

試行回数が非常に多い場合、その分布はつりがね型の「ベル・カーブ」になります。このベル・カーブは1733年アブラーム・ド・モアブルによって定義されました。

カール・フリードリッヒ・ガウスは、誤差の多い測定結果の修正に最小二乗法を用いました。そして真の値を計算する際に、誤差の分布を正規分布として計算しました。

1812年にピエール・シモン・ラプラスは最小二乗法、帰納的確率論、仮説の検証といった確率や統計の基礎を統合しました。「正規分布」という言葉はチャールズ・サンダース・パース、フランシス・ゴルトン、ヴィルヘルム・レキシスの3人によって1875年頃に導入されました。
 

正規分布は以下の式で表されます。図2に正規分布曲線を、表1に正規分布における信頼区間と誤差を示します。

信頼区間と誤差の理論は、今でも品質管理やシステムの信頼性の基本として広く用いられています。
 

例えば、目標値に対し測定結果の標準偏差が0.01ミリでした。

このとき信頼区間1σ、つまり±0.01ミリの誤差は31.7%
測定結果の31.7%は±0.01ミリの範囲外、つまり不合格になります。

このとき信頼区間3σ、つまり±0.03ミリの誤差は0.27%
測定結果の0.27%は±0.03ミリの範囲外、つまり不合格になります。

このとき信頼区間5σ、つまり±0.05ミリの誤差は0.000057%
測定結果の0.000057%は±0.05ミリの範囲外、つまり不合格になります。
 

このようにして品質管理では製品の信頼度を評価しています。そして高度な信頼性が求められる製品では、0.000057%の誤差でさえ問題になるのです。

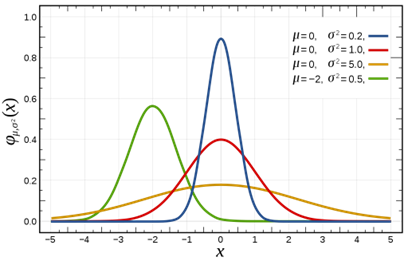
表1　信頼区間と誤差（σは標準偏差）

信頼区間	発生確率（％）	誤差（％）
1σ	68.2689492	31.7310508
2σ	95.4499736	4.5500264
3σ	99.7300204	0.2699796
4σ	99.993666	0.006334
5σ	99.9999426697	0.0000573303

 

ランダムさとは？

確率論の対象となる、このように必ずしも結果が決まっていない現象をランダム（random）といいます。これは以下のように定義されます。
「事象の発生に法則性（規則性）がなく、予測が不可能（英語版）な状態で、無作為性ともいう」

ランダムの例としてコイン投げやサイコロがあります。
実際は完全なサイコロやコイン投げは存在しません。そのため必ず結果に偏りが出ます。ただし物理では、予測が不可能であればランダムとします。
 

実際のカジノのルーレットも完全にランダムではありません。

1964年リチャード・ヤレキ氏は、記録係を8人雇い、ヨーロッパの何か所かのカジノに行かせました。そしてルーレットの出た数字をひたすら記録させました。そしてそれぞれのルーレットのくせを完全に把握すると、3,000万円の資金を借りてカジノに出かけました。

ヤレキ氏の荒稼ぎは半年続き、その間に7億4,000万円を手にしました。
カジノ側も荒稼ぎをするヤレキ氏に気づき、毎日ルーレット盤を変えました。しかしヤレキ氏はルーレット盤の僅かなキズや変色も記録しておいたので目当ての台を見つけました。
 

この一見ランダムな事象も長いスパンではあるパターン(傾向)がみられます。ひょっとするはこれがギャンブルの「運」なのかもしれません。
 

1950年フェラーはコイン投げを1万回行い、表と裏の出現頻度にパターンがあることを発見しました。
単純なコイン投げでも回数が多いと長期的なパターンがみられるのです。
 

数学者のベノワ・B・マンデルブロ氏は、このランダムさには複数の「状態」又は型があると言います。

• マイルド型
  コイン投げなど、平均値から一定の範囲内でゆらぐものです。自然界でもこれが正常な状態とされてきました
  
  
• ワイルド型
  極めて不規則に変化し、予測が困難
  
  
• スロー型
  マイルド型とワイルド型の中間

 

予想以上にランダム

19世紀の数学者コーシーは、ガウスとは異なった誤差理論(コーシー曲線)を考えました。

目隠しをしたアーチェリー選手の撃った結果は、時には外れ方が半端なく大きくなります。そして誤差は正規分布になりません。

たった1回でも大きく外すと平均値が大きく書き換わるため平均値は一定に収束せず、標準偏差は無限大になります。
 

ガウスは大きな変化はたくさんの小さな変化の結果と考えました。しかしコーシーは大きな変化は意外に高い確率で発生すると考えたのです。

 

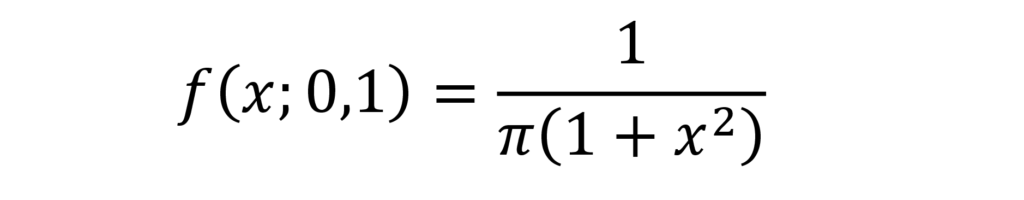
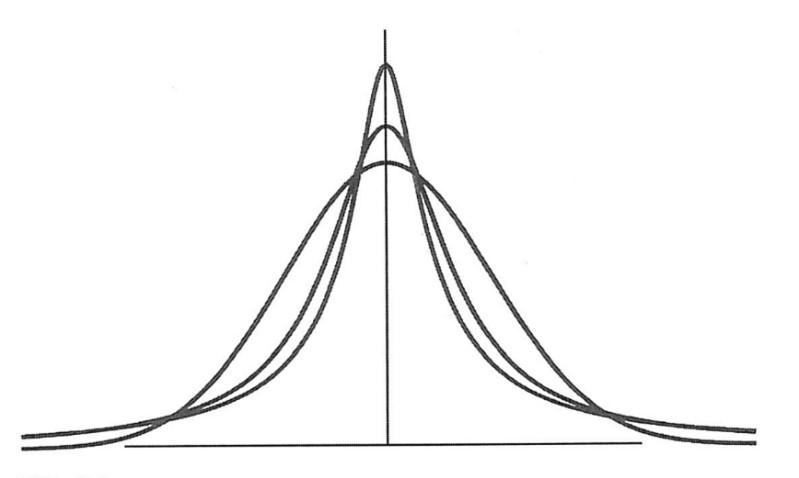
図4で、最も背の低い曲線が正規分布、最も背が高い曲線がコーシー分布の曲線です。

その中間の高さの曲線はマンデルブロ氏が調べた実際の市場における綿花の価格の変動の分布です。

当時は、多くの学者がガウスの理論はシンプルで現実的であると考えました。しかしマンデルブロ氏はむしろコーシーの理論の方が自然に見えると言います。
 

金融工学の誕生とその土台

確率論がギャンブルを出発点に発達しました。逆にギャンブル要素の高い金融市場(株式市場)に確率論を持ち込んだ人たちがいました。
 

株式市場は確率的？

フランスの数学者ルイ・バシュリエは、株式や債券の価格の変動がランダムウォークであると考えました。

この価格の変動に確率論を適用して1900年に論文「投機の理論」を書きました。ランダムウォークとは価格動向が確率的に等しく上下する（ボラティリティ）場合の振る舞いです。このランダムウォークの分布は正規分布で表現できます。

さらにバシュリエは債券価格の値動きに微粒子の不規則な動き「ブラウン運動」の理論を応用しました。
 

当時フランスでは株式以外にオプションやワラント債などが活発に取引されていました。バシュリエは実際にオプション取引や先物取引の価格付けに自分の理論を当てはめてみたところ、利益を上げた人の割合はバシュリエの理論と一致しました。

このときバシュリエは以下の2つを仮定しました。

• 価格の変化は過去の変化の影響を受けない
• 価格の変化は正規分布に従う

これを前提としてバシュリエのモデルに従って、逆の方向の値動きをする株式や債券を組み合わせれば、リスクに応じた収益性の高い金融商品の組合せ(ポートフォリオ)をつくることができます。これは現代の金融商品(例えば投資信託)そのものです。
 

しかし、不幸なことにバシュリエは生まれたのが早すぎました。生前は全く評価されませんでしたが、彼の理論は彼の死後、1950年代になってハリー・マーコヴィッツ、ウイリアム・シャープ、ポール・サミュエルソン、ユージン・ファーマらが取り上げました。
より洗練され高度化し、これが現代のファイナンス理論の基礎となりました。

ファイナンス理論は次の「効率的市場仮説」を前提としています。

• 常に多数の投資家が収益の安全性を分析・評価している
• 新しいニュースは常に他のニュースと独立してランダムに市場に届く
• 株価は新しいニュースによって即座に調整される
• 株価は常に全ての情報を反映している

現実はこの前提を完全に満たしておらず、金融理論は現実を一部無視した主観的な面があります。

一方、この理論はシンプルで使いやすく、大半の市場にはよく適合します。そのため、現在も金融業界で広く用いられています。

ところが稀に、現実はこの前提から外れ、大きな変動が発生します。
 

マーコヴィッツとCAPM

シカゴ大学のマーコヴィッツは、リスクとリターンの関係を表す数式に確率論を用いました。これを元に現代ポートフォリオ理論を考え現代の金融工学を確立しました。

また企業の株式のパフォーマンスを定量化するためにCAPM（資本資産価格モデル、Capital Asset Pricing Model）を考案しました。このCAPMは今も企業が投資先としての自社の価値を示すのに使用しています。
 

CAPMでは、ある株式に期待されるリターンは個別の株式が持つβ値とリスクフリー・レートから計算します。
E(r)　＝　rf　＋　β(rM－rf)
E(r)：　任意の株式の期待リターン
rf：　リスクフリー・レート(実際は国債の利回り)
β：　任意の株式のβ値
rM：マーケットが期待するリターン

CAPMから計算した株式投資期待収益率E(r)は、企業側から見れば株主コストです。
 

この株主コストと負債コストを加重平均すると企業が調達している資本のコスト（WACC、加重平均資本コスト）が計算できます。 このWACCで個別案件が生み出す将来のフリー・キャッシュフローを割り引けば、個別の投資案件の採算性が評価できます。

このβ値は企業の株式が市場全体の株価の動きよりも大きく変動するか、小さく変動するかを表します。つまりその株式のリスクを示します。大きなリターンを求める投資家はβの高い株式を狙い、リスクを嫌う投資家はβの低い株式を選択します。

1960年ウイリアム・シャープはマーコヴィッツに
「効率的市場仮説が正しいのであれば、効率的なポートフォリオは一つだけになるのではないか」
と尋ねたところ、彼の答えはイエスでした。これを実現したのがインデックス・ファンドです。
 

ブラック＝ショールズの公式

デリバティブなどオプションの価格は、すでにバシュリエが1900年の論文でオプションの評価式を考案しました。しかしオプションの価格評価の中で、リスクの市場価格を明示できなかったため実用性は乏しいままでした。

1965年にハーバード大学からアーサー・D・リトルに移ったフィッシャー・ブラックは、ワラント債の評価式を研究しました。そして1969年にワラントの評価式を導出しました。しかしブラックは方程式を解くことができませんでした。
 

ところが同じ1969年マサチューセッツ工科大学（MIT）に移籍すると、ブラックはこれが熱伝導方程式の一種であることには気付きました。そしてMITのマイロン・ショールズと共に評価式を完成させました。そして実際にこの評価式を使って割安なワラント債を買ってみたところ、この評価式はオプションの評価に十分使えることが分かりました。

そして1970年オプションの評価式としてこのブラック＝ショールズの公式を発表しました。これにより市場で取引されていたオプションやワラント債などデリバティブの適正な価格が算出できるようになりました。
 

Ｓ : 原資産である株式価格
Ｎ(α） : 正規分布に従う確率変数がα以下の値をとる確率、すなわち正規分布の累積分布関数
Ｋ : コール・オプションの行使価格
ｔ : 満期時点（年単位）
ｒ : オプションの満期に対応する無リスク金利（連続複利ベース）
ｅ-rt : 時点ｔで発生するキャッシュ・フローを、連続複利金利ｒで現在価値に引き直すための割引係数（ディスカウント・ファクター）
σ : ボラティリティ（原資産の収益率の標準偏差）
 

【背景】

1950年代、60年代はアメリカの黄金時代でした。企業は年々成長し株価は多くの銘柄で値上がりが続きましたしかし1971年ドルは変動相場制に移行し、その後到来したオイルショックの影響もあり、アメリカは長い不況に見舞われました。企業の成長も鈍化しました。一方1973年にはシカゴにオプション取引所が開設され、株式以外の金融商品の取引が活発になりました。そこでオプション価格の算定のニーズが高まりました。

1993年にショールズはロバート・マートンと共にヘッジファンド「ロングターム・キャピタル・マネジメント(LTCM)」に参画しました。LTCMは当初4年間に40%を超える平均年間利回りという驚異的な成績を上げました。そして各国の金融機関の資金など合わせて1000億ドルを運用しました。

しかしアジア通貨危機によるロシア債券価格の急落により経営破綻しました。ブラック＝ショールズの公式にはアジア通貨危機は盛り込まれていなかったようです。
 

経済学の流行

金融工学や経済学に対し、マンデルブロ氏は「伝統的な金融工学は以下の仮定に基づいている」と言います。

1. 人間は合理的に考え、豊かになることだけを目的としている
   《理論上は》　合理的に意思決定する
   《現実は》　意思決定は時には非合理(これは行動経済学で明かされた)
   
   
2. 投資家の行うことは全て似たり寄ったり
   《理論上は》　同じように行動する
   《現実は》　投資家の行動は同じではない
   
   
3. 株式や債券の価格が急変することはない
   《理論上は》　少しずつ変化する
   《現実は》　時には激しく変化する

 

金融工学が価格の変動をブラウン運動とみなして価格を算定するためには、以下の3つの理論上の仮定があります。

• 過去の価格は現在の価格に影響しない
• 価格の変動は統計的には定常性がある
• 価格の変動は正規分布に従う

しかし現実はそれほど単純ではありません。
 

ところが多くの経済学者は、単純なモデルを使ってきれいな結果を出すことを重視しています。そしてモデルが現実に合わない時は「アノマリー」(異常)とし、モデルを見直そうとはしません。

1. 金融モデルは市場の動きを正確に予想できるか
2. 現代ポートフォリオ理論に従えば安全で利益を出せる投資戦略が立てられるか
3. 金融アナリストやCFOはCAPMを利用して正しい判断をしているか

 

「この3つ問いの答えがイエスならモデルの妥当性に文句をつけるべきではない」
とアメリカの経済学者ミルトン・フリードマンは述べています。

稀に起こる突発的な変化を「アノマリー」として除外すれば金融工学のモデルは実用的で現実に十分適合します。

ただし、それは「突発的な変化による被害が自分に及ばない時」に限ります。
 

カオス理論が明かす想定外の変化

カオスとは「混沌」を意味する英語で、語源はギリシャ語のkhaosです。

これは宇宙が成立する以前の秩序なき状態を意味します。
 

カオス理論のカオスは、数学用語です。これは「決定論的システムにおける確率論的なふるまい」を意味します。

これはどういうことでしょうか？
 

カオス理論とフラクタル

フランスの数学者アンリ・ポアンカレは、
微分方程式の解が一つだけ決まるということは、その運動が何度も繰り返す、つまり周期性を持っている
ということを発見しました。
 

トポロジー(位相幾何学)

トポロジーは数学の一分野です。
何らかの形（又は「空間」）を曲げたり伸ばしたり(切ったり貼ったりはしない)しても保たれる性質のことです。このトポロジーは、空間、次元、変換といった概念の研究から生まれました。

オイラーの多面体公式が知られ、20世紀中頃には数学の著名な一分野になりました。

 

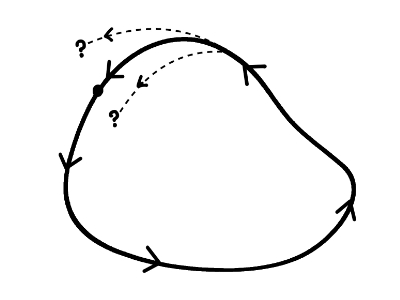
位相空間の中でひとつの点が閉曲線に従って運動すれば、その点は同じ運動を永久に繰り返します。

 

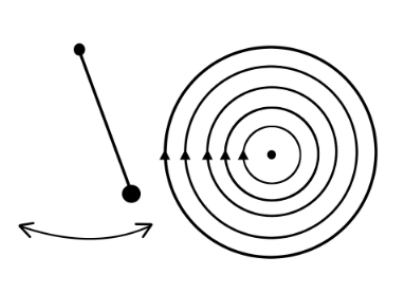
図7は理想化された線形運動である振り子の位相空間線図です。振り子の振動は円を描きます。この円の大きさは、初期条件によって変わります。

実際の振り子の運動の位相空間線図は非線形のため、理想化された線形運動のものとは大きく異なります。
 

ポアンカレ断面

微分方程式の解が一つだけ決まる場合、その運動は周期性があります。その場合、曲線は必ず出発点に戻ってきます。

ポアンカレは、位相空間の中で、周期運動する軌跡が出発点と同じ位置に戻ってくる断面をポアンカレ断面と呼びました。つまりポアンカレ断面があれば、その運動方程式は周期解が必ず存在するということです。

 

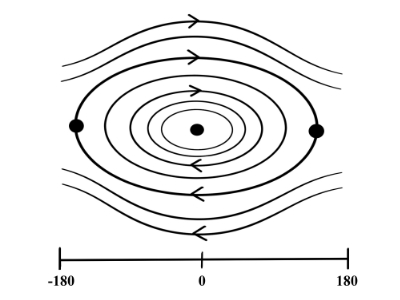
カオス理論

決定論とは
「初期値を与えると必然的に未来での振る舞いが与えられる」
ことです。

決定論的なふるまいをする事象が非線形の場合、初期値がわずかに異なっただけで予想できない不規則な現象が起きます。
これをカオスと呼びます。

 

ある事象がカオスかどうかの判定はフラクタル次元というものを使用します。

フラクタルは、カオスの逆プロセスのことです。そしてある事象のフラクタル次元が「非整数」であればカオスです。
 

例えば生物の数の増加を示す微分方程式の解は、最初急激に増加した後、ある値に収束します。

しかし実際の生物の増加は、連続的でなく離散的です。そこでこの微分方程式を差分方程式に変換します。すると解は、定常状態から周期状態、さらに不規則な状態へ変化を続けます。
これがカオスです。
 

ストレンジ・アトラクター

アトラクターとは「何かを引きつけたり、吸い寄せたりする」という意味です。
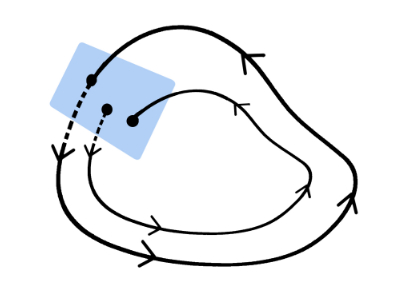
カオス軌道を位相空間にプロットすると不思議な形になります。ループやらせんが合流せず、決して交わりません。これをストレンジ・アトラクターと呼びます。

ストレンジ・アトラクターは無限の細部構造を持っています。その一部を拡大すると同じ様な細部構造が現れます。つまり自己相似性質があります。(フラクタル)

 

バタフライ効果

バタフライ効果とは、力学系のわずかな変化により、その後の系の状態が大きく異なってしまうことです。

気象学者のエドワード・ローレンツの
「蝶がはばたく程度の非常に小さな撹乱でも遠くの場所の気象に影響を与えるか?」
という問いからバタフライ効果と呼ばれるようになりました。

ローレンツの研究では観測誤差をゼロにしない限り正確な長期予測は困難という結論に達しました。

 

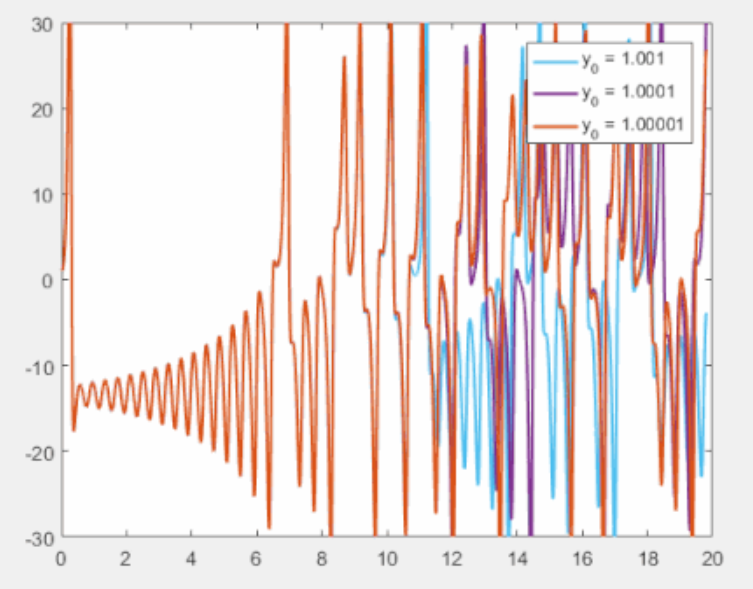
ローレンツ方程式における初期値鋭敏性（バタフライ効果）の例。横軸は時間、縦軸はある変数の変化を示す。水色は初期値 1.001、紫は 1.0001、朱色は 1.00001 で、最初のころはほとんど同じ動きだが、ある程度時間が過ぎたところで全く違った動きになる。(Wikipediaより)
 

バタフライ効果の例
一方バタフライ効果は、ローレンツが研究・発表した3元連立非線形常微分方程式(ローレンツ方程式)が生み出すストレンジ・アトラクターの形状に由来するという意見もあります。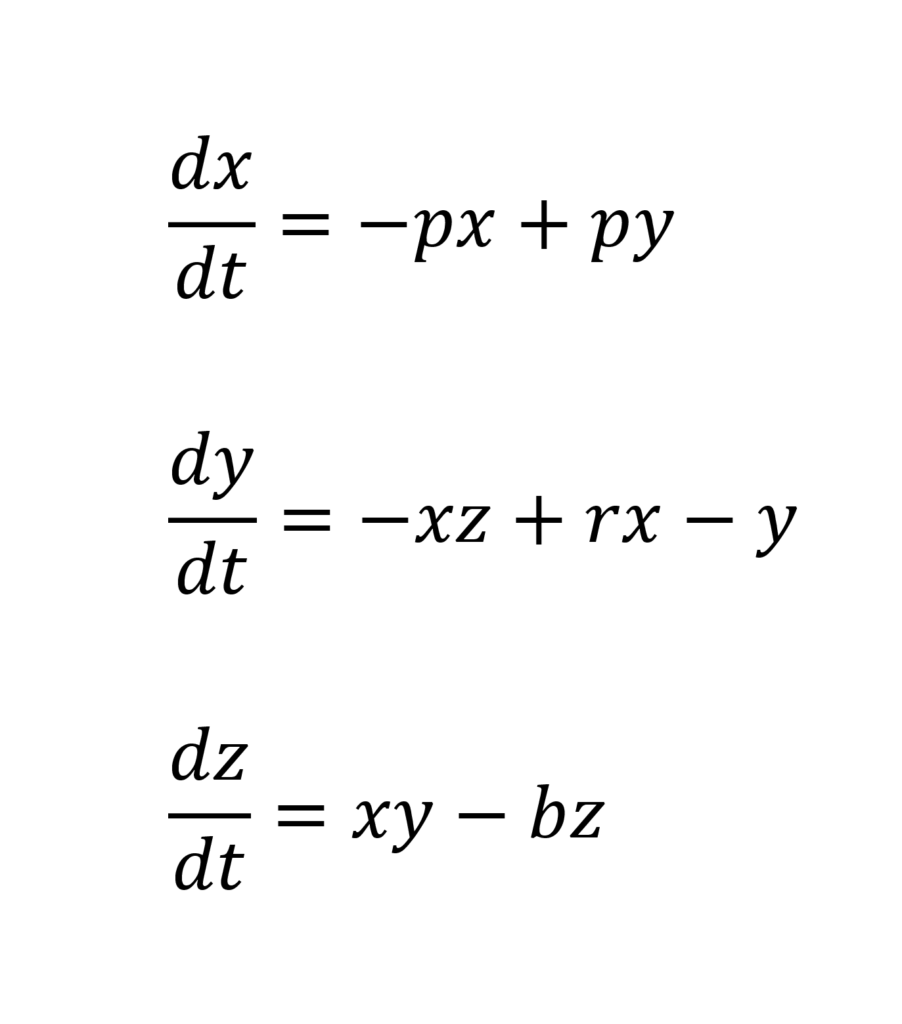

 

フラクタル

フランスの数学者ブノワ・マンデルブロが提唱した幾何学の概念です。図形の部分と全体が自己相似になっているものを指します。
 

具体的な例に海岸線の形があります。一般的の地形は複雑な図形でも拡大すれば滑らかな形状になりますが、海岸線はどれだけ拡大しても同じように複雑な形状が現れます。

そのため海岸線の長さは、小さい物差しで測れば測るほど微細な凹凸が測定されて長くなります。つまり図形の長さは無限大になってしまい、無限の精度を要求されれば測ることはできません（海岸線のパラドックス）。

フラクタル次元はこの様な図形を評価するためのものです。
 

比較的滑らかな海岸線のフラクタル次元は線の次元1に近く、リアス式海岸のような複雑な海岸線のフラクタル次元はより大きな値になります。なお、実際の海岸線のフラクタル次元は1.1 – 1.4程度とされています。以下はフラクタル図形の例です。これらの図形はすべて数式が表されています。

 

自然界の不均衡

生態学のA・J・ニコルソンはアオバエの個体群の大きさを研究しました。
容器の中でアオバエを繁殖させると、1万匹まで増えて容器は一杯になります。個体数は急激に減少します。

そしてある程度減少すると空間に余裕ができ、個体数は再び増加します。
 

このサイクルは38日で繰り返されますが、前と同じになることはなく、周期的に揺らぎます。
伝染病の流行もカオス的なものが見られました。イングランドとウェールズの風疹患者の時系列(1948－1966年)での増減もカオスとしてモデル化できました。
 

カオス理論で品質を改善

1994年SRAMA(バネ研究製造協会)のレン・レイノルズは、バネの品質を安定させるには素材の加工性が重要だと考えました。

そこでバネのテストサンプルをつくり、出来上がったバネのピッチを測定しました。この測定データが時系列に変化することに着目して、カオス理論のリュエル・ターケンスの位相空間再構成を使ってアトラクターを図式化しました。

このアトラクターには、巻取り性の良い線材とそうでない線材の違いをはっきりと示しました。
 

そこで新たに補助金を使ってSRAMAとウォーリック大学数学研究所は共同でFRACMATテストマシンを開発しました。

このテストマシンは、コンピューターによってデータを統計分析、およびカオス理論分析を行い、弾性/摩擦線の連続変動を定量化しました。

これによりワイヤー製造者は高品質のワイヤーを確実に顧客に提供できました。スプリングメーカーは、一貫性のないワイヤーを排除したことでセットアップの時間が短縮されました。
 

想定外に戸惑わないために

近代科学の幕開けは、ニュートンによって世界をシンプルな数学で表したことです。
しかしその過程で複雑な自然現象を解析的に解くために、現実から乖離したモデルに修正しなければなりませんでした。

この前提条件に気づかずに複雑なシステムを構成すると、自然界本来の姿がモデルと違った姿を現した時、モデルは瓦解し、私たちは戸惑います。

「想定外！」、これが原因かもしれません。

 

もっと安全が必要

マンデルブロ氏は、金融工学が前提となっている正規分布にも疑問を持っています。
そして実際に正規分布でないものはとても多く存在します。

 

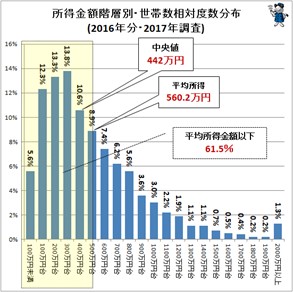
イタリアの経済学者パレートはスイス、ドイツ、イギリスなど様々な国の税金の記録などを調べ、所得の分布をグラフ化しました。

驚くべきことにどのデータも偏っていて正規分布ではありませんでした。図15は日本の世帯ごとの所得分布です。
 

いつの時代も富は一部の特権層に集中していて、最も多い中間層は上に上がる可能性もあれば、最下層に落ちる可能性もあります。そして一定の最下層は劣悪な環境に置かれます。これは正規分布でなくべき乗分布です。その結果、所得の平均値はわれわれの実感とは乖離しています。
 

長期にわたる価格変動のデータとして、マンデルブロはアメリカの綿花の価格に注目し、100年分のデータを分析しました。その結果、価格のゆらぎ(ボラリティ)はバシュリエの理論とは大きく異なっていました。

データを増やすと標準偏差は大きくなりました。つまり正規分布よりも大きなゆらぎがあったのです。

そこで対数でプロットすると直線状になりました。つまりこれもべき乗分布でした。
また価格の日次、月次、年次の変化をプロットするとか、どれも似ていました。つまり大きな変動が発生する割合はどの時間スケールでも同じでした。このような変化はフラクタル的、つまりカオス的でした。
 

1906年ハロルド・エドウィン・ハーストはナイル川の水不足に対処するために過去の洪水の記録を調べました。そして、どのくらいの容量のダムが必要か調査しました。

調査の結果、洪水と干ばつはランダムに起きるのでなく、洪水が起きれば翌年も洪水が起きる「長期記憶性」がありました。ハーストは他の河川のデータも調べて、どの河川にもある公式が当てはまることを発見しました。その結果、変動の幅は、時間の平方根(0.5乗)で広がるのでなく、3/4乗(0.75乗)で広がりました。

 

これをハーストは自然の本質的な性質と断定しました。
 

マンデルブロ氏の金融への提言

マンデルブロ氏は、市場価格は乱高下するものと考え、以下のように提言しています。

• 金融市場の価格は正規分布でなく、ワイルド型で変動する乱流であり、変動は集中し不連続で急激に変化する。変化が大きければ市場のリスクは極めて高くなる。
• 市場が乱流のため、既存の金融理論(正規分布)では起こるはずのないリスクが現実には起こる。従ってどの株式に投資するかよりも、株式、債券、現金にどのように配分するかの方が重要。
• 特に市場のタイミングは重要。巨額の利益と損失は極めて短時間に起きるため、「すぐに買って、すぐに売る」ことが良い結果を生む。
• 価格は不連続にジャンプし、それがリスクをより高くする。些細な情報で投資家が行動するとそれが大きな変動をもたらす(バタフライ効果)。そのため価格は不連続に大きく変動する。
• 市場における価値は限定された価値。経済アナリストは企業の年次報告書から企業の価値を推定し、あるいはそれぞれの国のインフレ率や金利から為替レートを推測する。しかしワイルドに価格が変動するものの価値を算出できるだろうか。

実は固有の価値の根拠はありません。それなのにあたかも価値が算定できるかのような取組は、多くの問題を抱えることとなります。
 

自然界の予測不可能性

金融工学では、前提条件が現実と合ってなく、前提条件を正規分布と仮定したため、実際の価格の変動はもっと大きくなります。さらに価格の変動は長期記憶性があるため、長いスパンで増加や減少が続きます。そしてこれがバブルを引き起こします。
 

これを自然界に当てはめて考えると、我々が解き明かしたと思っていた自然現象、例えば、
音響、振動、運動、流体、物体の変形なども、現実を無理に線形微分方程式に置き換えたものが多いことに気付かされます。しかし実際の自然現象は非線形が多くあります。つまり使っているモデルが現実に合いません。

こういった非線形の問題を解決するアプローチとしてカオス理論は今後有望です。

 

特に長い期間の変動には長期記憶性があるため、正規分布モデルは不十分です。十分に安全を確保するならば、堤防はもっと高く、ダムの水はもっと多く、防潮堤はもっと高くしなければなりません。また例え解くことができた線形微分方程式でも、初期条件のわずかな変動により結果が大きく変わることがあります。
 

工学でも誤差の解析は正規分布を前提としています。では、その前提条件は本当に合っているのでしょうか。分布が異なれば、結果は違うものとなります。

長期的に堅牢なシステムをつくるには

• 長期スパンでの変動を考慮
• 僅かな初期条件の違いによる結果の影響を考慮
• 正規分布などの前提条件が間違いないか、検証

このような取組が必要です。
 

参考文献

「禁断の市場」　ベノワ・B・マンデルブロ　著　東洋経済新報社
「カオス的世界像」　イアン・スチュワート著　白揚社
「複雑系を超えて」　上田 睆亮、稲垣 耕作、西村 和雄著　筑摩書房
 

本コラムは「未来戦略ワークショップ」のテキストから作成しました。

中小企業ができる簡単な原価計算手法

書籍

「中小製造業の『原価計算と値上げ交渉への疑問』にすべて答えます！」

「原価計算」と「値上げ交渉」について具体的に解説した本です。
原価計算の基礎から、原材料、人件費の上昇など原価に与える影響がわかります。取引先との値上げ交渉のポイントも解説しています。実務担当者から管理者・経営者に役立つ内容です。

「中小製造業の『製造原価と見積価格への疑問』にすべて答えます！」

「この見積価格は正しいのだろうか？」「ランニングコストはどうやって計算するのだろうか？」多くの製造業の経営者や管理者が感じている「現場のお金」の疑問についてわかりやすく書した本です。
切削加工、プレス加工の架空のモデル企業を使って、アワーレートや見積金額を具体的な数字で示しました。難しい会計の理論はないので、会計の苦手な方も抵抗なく読めます。

「中小企業・小規模企業のための個別製造原価の手引書」【基礎編】【実践編】

中小企業が自ら製品の原価を計算する手引書として、専門的な言葉を使わず、できる限り分かりやすく書いた本です。「難しい会計の知識は不要」「原価計算の専任者がいなくても事務や経営者ができる」ことを目指して、
【基礎編】はアワーレートや間接費、販管費の計算など原価計算の基本について書きました。
【実践編】は具体的なモデルを使ってロットの違い、多台持ちなど実務で起きる原価の違いや損失について書きました。