「人工知能AIの発達で仕事はどう変わるのか」 ～その1 知能とは何か？AIの知能は人を超えるのか？～
今、再び人工知能が脚光を浴びています。
この人工知能について考える際、知能とは何かを明らかにする必要があります。
知能とは何でしょうか？
人の知能の源は心です。私たちは心により世界を認識します。
この「人は世界をどのように考えるか」は哲学の世界です。
プラトンの二元論
ギリシャの哲学者プラトンは、彼の打ち立てたイデア論において世界は二つ存在します。
ひとつは目に見える世界です。
もう一つは目に見えない理想的な形(イデア)の世界です。
プラトンによれば、このイデアではすべてが論理的に一貫した矛盾のない世界で、これはすべて数学によって表すことができます。この理想的な世界がまずあり、私たちが暮らす現実の世界はその投影にすぎません。
従って様々な概念、思想を数学によって論理的に一貫して説明できれば、それを投影したものが現実の世界にあるはずです。
図1 プラトンのイデア論
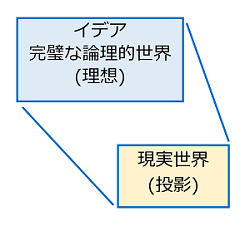
この「すべてが論理的に矛盾のない首尾一貫した世界」という概念は、その後の西洋の哲学、思想、科学における基本的な概念として広く浸透しました。さらに今日の人工知能研究者に大きな影響を与えました。
一方、プラトンの弟子であるアリストテレスは「物事の本質は自然界の調査を通じて明らかになる」という経験主義を打ち立てました。このアリストテレスの経験主義は広く受け入れられ、多くの人が実験・実証を基に科学的な探求に取り組み、科学の大いなる発展をもたらしました。
つまりガリレオが地動説を確信したのは教会で瞑想したからではありません。「経験主義」に基づきひたすら望遠鏡をのぞき観察したからです。
科学から協会の足かせを外す
17世紀の哲学者デカルトは、それまでの「神と聖書」という絶対的な権威に変わり、個人にとって「何が確かなものか」を思索し続けました。そして
「我思う、ゆえに我あり」
という結論に達しました。
唯一確かなことは、今このことを思考している自分の心です。
こうしてデカルトは、肉体的存在(レス・エクステンティア)と精神的存在(レス・コギスタンス)を分離しました。
このデカルトの二元論によって科学は協会からの足かせを外され、科学者は
「世界は何からつくられているのか」
「どうしてすべてのものは今のような姿になったのか」
肉体的存在(レス・エクステンティア)を自由に探求できるようになりました。
図2 デカルトの二元論
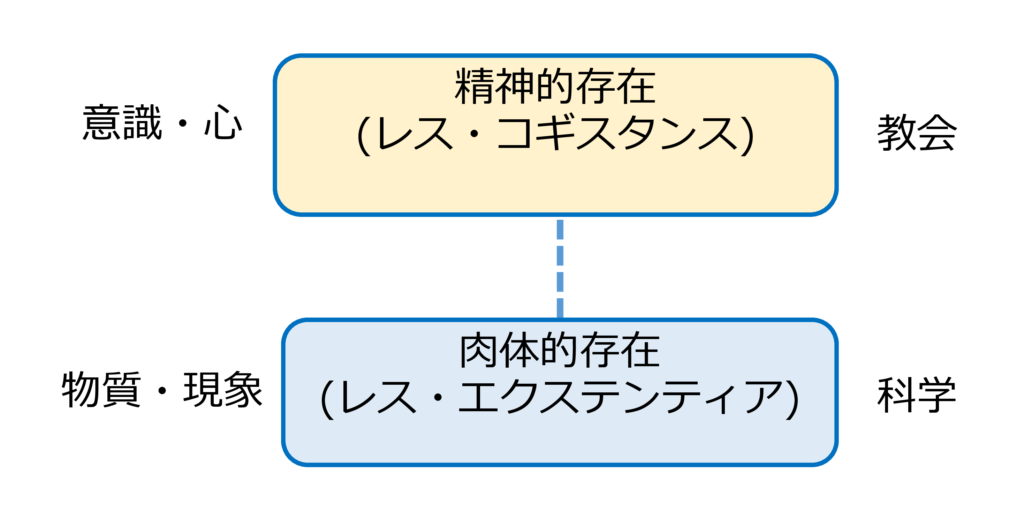
その一方、精神的存在(レス・コギスタンス)はその後も教会の市墓にありました。心の問題は科学から置き去りにされてきました。こうして「どのようにして心が体に物理的な影響を及ぼすのか」という「心身問題」は20世紀に至るまで長い間の課題でした。
意識のハードプロブレム
私たちは赤いリンゴを見れば「赤い」と思います。
リンゴの形は網膜に投影され、視神経から脳に送られます。同様に色の情報も脳に送られます。
しかし、なぜその情報を私たちは赤いと思うのでしょうか。
デカルトの二元論に基づく人たちは、意識にクオリア(感覚質)というものが存在すると考えました。つまり心とは単なる脳細胞の神経伝達物質の移動という物理現象でなく、目に見えないクオリア(感覚質)によるものと考えています。
図3 クオリア
デビッド・チャーマーズはこのクオリアの解明を「意識のハードプロブレム」と呼びました。そして脳科学や生物学で研究されている課題「イージー・プロブレム」と比較し、クオリアの解明は解決困難な問題としています。
西洋の論理学
論理学とは、人間の推論についての形式や構造を研究する学問です。有名なのは演繹法や帰納法があります。論理学ではある事実を「命題」と呼びます。
アリストテレスは、複数の命題を組合せることで、正しい推論に達する方法を探求しました。
例えば三段論法は
「ソクラテスは人である。」
「人は死ぬ。」
よって「ソクラテスは死ぬ。」
という結果を得ます。
このような推論の方法には演繹法や帰納法があります。
演繹法
真理をつないで推論を重ねる方法です。
三段論法も演繹法の一つです。
帰納法
個別の事実から一般的な法則を見出す方法です。
演繹法では前提が真であれば結論も真ですが、
帰納法では前提が真でも結論が真とは限りません。
論理を数式化! ブールの功績
この論理学を19世紀ジョージ・ブールは、言葉の代わりに数学の演算規則をあてはめ、代数式で記述する方法を考えました。（ブール代数）
ブール代数により頭の中で考えた論理的な思考を数式であらわすことができるようになりました。この数式は真と偽を1と0で表すため、コンピューターで処理ができ、後のコンピューターの演算の基礎となりました。
図4 ブール代数
記号論理学の確立
さらにゴットロープ・フレーゲは、ブール代数で表現ができなかった多義的な表現を表す方法として、変数を含む述語論理という方法を発明しました。こうして論理表現の世界を大きく広げました。
フレーゲは述語論理に基づいて世界のありさまを分析的に記述することを目指しました。こうしてプラトンの考えたイデア(論理的に一貫した完全な世界)を実現する体系ができました。
この形式論理体系は
- 体系内で他の真実と矛盾する真実があってはならず、首尾一貫していなければならない
- 体系内では真の前提から偽の推論を導いてはならない
- 体系内のある文が真なら、そのことを証明できなければならない「完全性」
となるはずです。
そこでドイツの数学者ダフィット・ヒルベルトは記号論理学を完成させるために世界中の数学者に
- 「数学において真である命題は必ず証明できること」
- 「公理から形式化された推論をどれだけ行っても、矛盾が示されることは絶対ないということ」
を証明してほしいと依頼しました。
このヒルベルトの「決定問題」によれば、以下のことが実現すると考えられました。
ある文を入力した時、その文が真かどうかを判定するアルゴリズムを示すことができれば、
それを実行する機械はあらゆる定理を証明する完全な論理的機械となる。
しかし1930年オーストリアのクルト・ゲーデルは
「『矛盾が起こるような命題が存在しない』とは、その理論によっては証明できない」
ことを彼の「不完全性定理」の中で証明しました。
これによりヒルベルトの「決定問題」は実現困難であることが証明されました。
図5 論理学体系
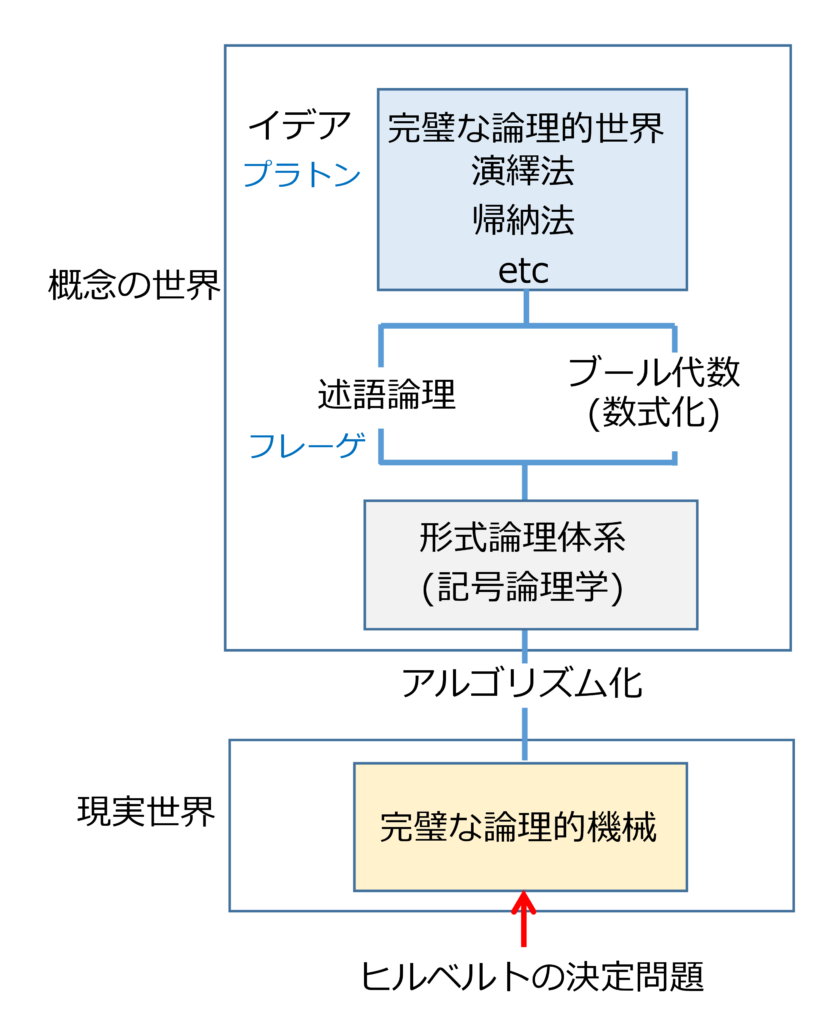
このように「完全に首尾一貫した論理で表現した理想の世界」に対する西洋の哲学者、科学者の執念は、ブール代数や記号論理学の発展をもたらしました。そして論理学は今でも欧米の大学などでは重要な一般教養科目となっています。
それはまたあらゆる定理を証明する完全な論理的機械を求めることにもなりました。それを実現する機械は、別の要求から急速に発展しました。
17世紀から19世紀にかけて機械仕掛けの自動人形オートマタがヨーロッパで流行しました。音楽は生演奏しかなかった時代、機械仕掛けで音楽を演奏するオートマタは人々の楽しみでした。
計算機の誕生
1642年フランスのブレーズ・パスカルは歯車式計算機「パスカリーヌ」を考案しました。しかし加減算しかできなかったため売れませんでした。
ドイツの数学者ゴットフリート・ライプニッツは、独自の機構ライプニッツ・ホイールにより乗除算もできるようにパスカリーヌを改良しました。この改良した計算機は、その後60年間で1500台が販売されました。
またライプニッツは1698年に二進数の理論を確立しました。
図6 ライプニッツの計算機(Wikipediaより)
幻のバベッジ機関
1822年イギリスのチャールズ・バベッジは計算機の乗除算(掛け算、割り算)が繰り返し計算であることに着目しました。そして階差方程式を使って繰り返し計算ができる階差機関の実験モデルをつくりました。
当時繊維機械は複雑なパターンの制御にパンチカードを使っていたことに着目しました。(現在でもパンチカード式のジャカード織機は使われています。)そこで計算プログラムをパンチカードに入れ、プログラムと機械を分離したバベッジ機関、つまり現在のコンピューターの基本となるものを考案しました。しかしバベッジは政府から多額の予算を受けながら開発はなかなか進まず、バベッジは完成する前に亡くなりました。
戦争が高めた計算機のニーズ
20世紀に入り第二次世界大戦が起きると高速計算のニーズが高まります。
ひとつは暗号解読です。暗号は複数の文字や数字の組み合わせから成り、その組み合わせを総当たりで調べるには、人よりはるかに高速で行う必要があります。この「総当たりで調べると時間がかかりすぎて解けない」という原理は現在のコンピューターの暗号技術も同じです。
もうひとつは大砲の弾道計算などで微分方程式を高速で解く必要がありました。
こうしてイギリスはドイツの暗号機「エニグマ」の暗号を解読するために、1943年1,500本の真空管を備えた世界最初のコンピューター「コロッサス マークⅠ」を開発しました。しかしイギリスは「コロッサス マークⅠ」の存在を最近まで秘匿していました。そのため世界最初のコンピューターとして広く知られているのは、アメリカの「ENIAC」です。
アメリカは1946年にコンピューター「ENIAC」を開発しました。これに関与していたのが天才的な頭脳を持つといわれたフォン・ノイマンでした。プログラムとデータをいったん記憶し逐次読みだして処理するコンピューターの原理は今も変わらず、この原理は「ノイマン型コンピューター」と呼ばれています。
孤高の天才チューリング
世界最初のコンピューター「コロッサス マークⅠ」の開発メンバーの一人が天才数学者アラン・チューリングでした。
チューリングはライプニッツの論理学に啓発され、「コロッサス マークⅠ」のはるか以前に、記号論理処理できる機械「チューリングマシン」を考案しました。
これはメモリ、演算機、記憶装置を備え、現在のコンピューターそのものでした。そして
「チューリングマシン」で処理できることはアルゴリズムで表すことができる
ことを数学的に証明しました。
さらに
「任意のアルゴリズムがいつ停止するのか」事前に決定するアルゴリズムはない
という「チューリング不完全」を証明しました。
これは論理推論を行って文の真偽を判定できる形式言語は存在しない
ことを示し、ヒルベルトの決定問題に対する決定的な反証となりました。
チューリングは、またコンピューターと知能について思索を深めていて
「機械は思考することができるか」を見分けるテスト
「チューリングテスト」を考案しました。
このテストは人間の審査員が1人の人間と1台のコンピューター(プログラム)に対して対話を行い、審査員が人間とコンピューターと区別がつかなかった場合、コンピューターは知能を持っていると判定する方法です。
このチューリングテストの効果について様々な意見がありますが、2014年にはロシアのチャットボット「ユージーン・グーツマン」がこのテストに合格しました。
図7 計算機の歴史
コンピューターの発展と人工知能ブーム
1946年にENIACが開発され、それ以降コンピューターは急速に進歩、発展しました。
1950年代には、IBMなどがコンピューターを商品化し、各国の研究機関や大学に設置されるようになりました。
こうして暗号解読と弾道計算から始まったコンピューターは、科学の進歩とともに高速での計算を求める分野に盛んに利用されるようになりました。
こうしてコンピューターが広く利用されるようになると、記号論理学で考えられていた「あらゆる定理を証明する完全な論理的機械」の実現可能性が出てきました。
第一次人工知能ブーム
1956年ダートマス大学のジョン・マッカーシーは「人工知能（Artificial Intelligence）」に関する会議を主催し、マービン・ミンスキー、ネイサン・ロチェスター、クロード・シャノンらが参加しました。
この会議でアレン・ニューウェルとハーバード・サイモンは、初めての人工知能プログラム「ロジック・セオリスト」のデモを行い、有名な数学の本「数学原論」の定理をいろいろな公理をしらみつぶしに組み合わせて証明できることを示しました。こうして数値計算しかできなかったコンピューターが記号論理学を証明できることが分かりました。
プラトンに始まり、フレーゲ、ヒルベルトにつながる記号論理学では、複雑な論理問題を解決できることが知性と考えられていました。そしてデカルトの二元論以来、意識や心は科学の外に置かれていました。
当時、コンピューター学者、数学者などの科学者は「あらゆる定理を証明する完全な論理的機械」が実現できれば、それは人工知能と考えました。そして意識や感情は、重要ではない動物的な側面と考えました。
そしてコンピューターが複雑な論理問題を自ら解決できるようになり、今後コンピューターの性能が上がりより複雑な問題をより速く解決できれば、いずれ人間の知能を追い越すと当時のコンピューター学者は考えました。
当時は東西冷戦下の影響もあり、遅れを取るまいと人工知能の開発には多額の予算がつき第一次人工知能ブームが訪れました。
第一次人工知能ブームの挫折
しかしこの第一次人工知能ブームは2つの障害により挫折しました。ひとつは「指数爆発」もうひとつは「フレーム問題」です。
指数爆発
現代情報理論の基礎を構築したクロード・シャノンは、1949年に「チェスのためのコンピュータプログラミング」を発表しました。
シャノンのミニマックス法は、どの状態が自分にとって有利かを示す評価関数をつくり、自分と相手の交互の打ち手の組合せのすべての評価関数の結果から最適な打ち手を決定する方法です。
図8では白は今1, 2, 3の3つの選択肢があります。白が打った後、黒はそれぞれ1, 2の選択肢があります。その結果2手先には6つの結果があります。それぞれの評価関数の結果を青で示しました。その結果、白は1を選択すれば、次に黒が1でも7、2でも12となり、他の手よりも結果の平均は高くなります。(MAX) 一方白が1を選択すれば次の手の評価関数は7となり、白には最も高い評価ですが、黒にとっては最も低い評価です。(MIN) こうして最初の手は1が選択されます。
一方この方法は、はるか先までの打ち手を先読みしようとすると、組合せが指数関数で増加し、コンピューターの計算能力を超えてしまいます。
図8 ミニマックス法
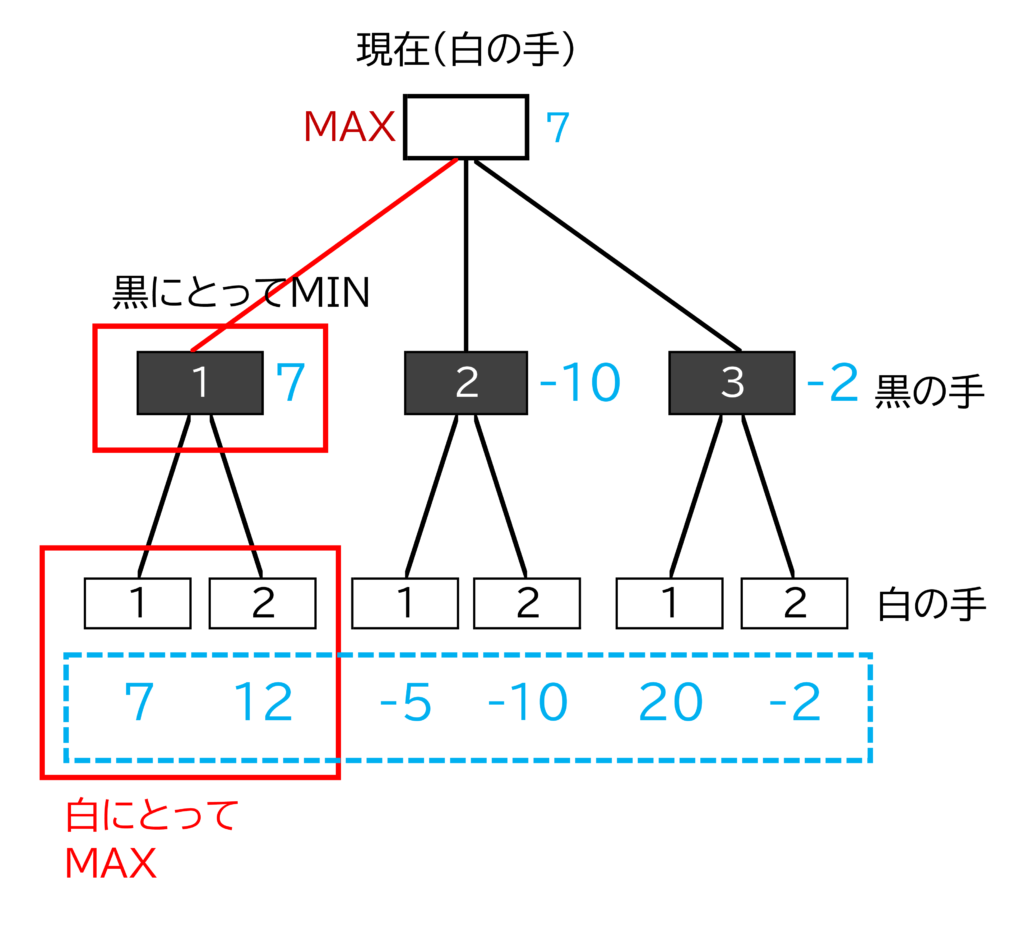
この探索空間の指数爆発は、コンピューターでは手に負えない問題です。
図9 組合せと計算回数
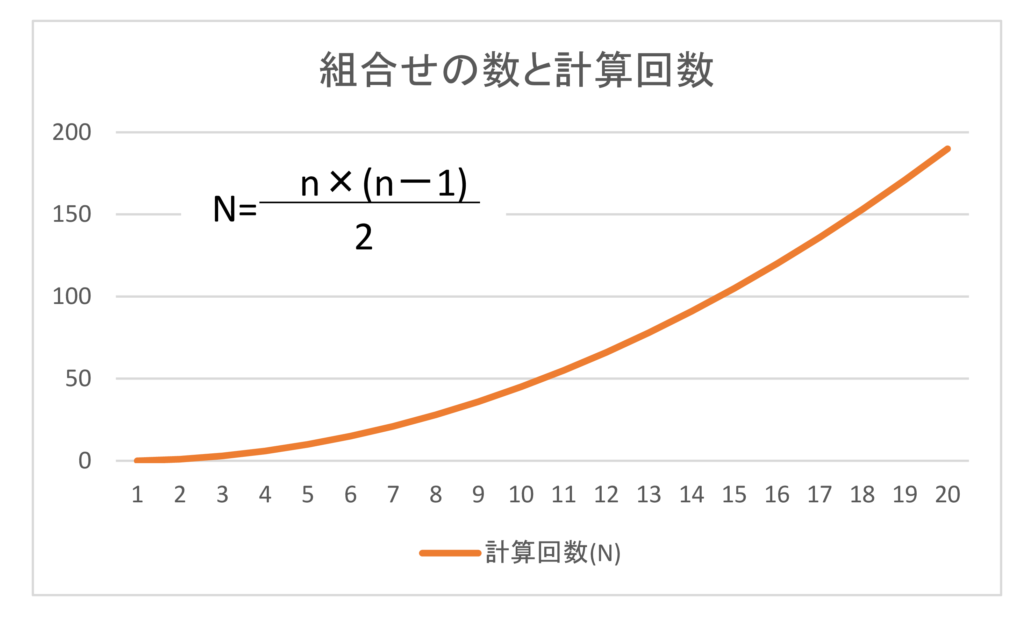
しかしカーナビは地図上で最短経路を示す必要があります。もしすべての組み合わせを計算すれば指数爆発を起こします。
1959年エドガー・ダイクストラは、スタート地点から一斉にスタートし、最も早くゴールに着いた経路が最短経路であるというアルゴリズム(ダイクストラ法)を考案しました。これは現在にカーナビに広く使われています。
一方よく似た問題で「巡回セールスマン問題」があります。
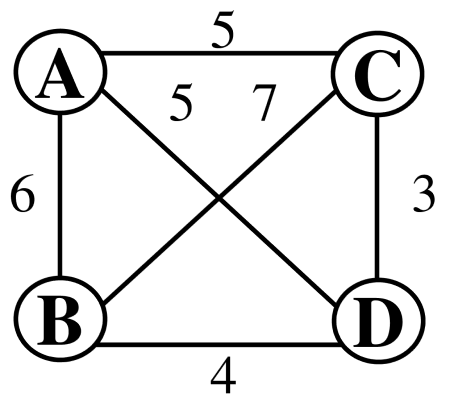
図10 巡回セールスマン問題
これは各都市とそれらをつなぐルートがわかっている時、これらの都市を全て通ってスタート地点に戻るルートのうち、最短のルートを求めるものです。
この問題は必ず指数爆発を起こすため、「NP困難な問題」と呼ばれています。
【実は計算できないゲーム理論】
「囚人のジレンマ」で知られるゲーム理論は、利己的なプレイヤーが自分の得になる事を優先して行動した場合、お互いの利害がどうなるかを示した理論です。
ここで相手がどのように戦略を変えても自分が得られるものが大きくなる条件が「ナッシュ均衡」です。これは経済学の教科書ではおなじみですが、実はナッシュ均衡の計算は指数爆発を起こします。そのためプレイヤーが多い場合のナッシュ均衡は理論上存在しても「計算できない」点です。
2009年にクリストス・パパディミトリウらがナッシュ均衡はNP困難な問題であることを証明し、現実的な時間内に答にたどり着くことは不可能であることを示しました。
適当に考えられない「フレーム問題」
1969年のジョン・マッカーシーが提言した問題で、コンピューターは問題を処理する際に全ての可能性を考えてしまうため、時間内に問題を処理できない問題です。
これに対して人間は結果に大きな影響を与えない事柄は取り除き、枠(フレーム)をつくって必要な事柄だけを枠の中に入れ、その中だけで思考します。
爆弾処理ロボットの悲劇
哲学者のデネットがこのフレーム問題を説明した例です。
【爆弾処理ロボット１号の悲劇】
人工知能搭載の爆弾処理ロボット１号は、人間の代わりに爆弾が仕掛けられている部屋から貴重な美術品を取り出す指令を受けました。爆弾処理ロボット１号は美術品が入った台車を押して部屋から出てきましたが、爆弾は台車に仕掛けられていたため、爆弾処理ロボット１号は爆発に巻き込まれました。
爆弾処理ロボット１号は美術品を取り出すために荷車を押せばよいことは分かったのですが，それによって，爆弾も一緒に取り出してしまうということは分からなかったためでした。
図11 爆弾処理ロボット1号
【爆弾処理ロボット2号の悲劇】
そこで改良した爆弾処理ロボット2号が製作され、再び美術品を取りに部屋に向かいました。爆弾処理ロボット2号は台車を動かしたときの影響を
もし台車を動かしても，天井は落ちてこない．
もし台車を動かしても，部屋の壁の色はかわらない．
もし台車を動かしても，部屋の電気は消えない．
もし台車を動かしても，壁に穴があいたりしない．
‥‥‥‥
と順番に考えている間に爆弾が爆発しました．
図12 爆弾処理ロボット2号
台車を動かしても天井は落ちてくることはないのですが、落ちてこないかどうかは爆弾処理ロボット2号は
「考えない」
とわかりません。
そして考えなければならないことは無数にあり、考えるのに時間がかります。その間に爆弾が爆発してしまいます。人間は影響のなさそうなことは考えずに排除しますが、コンピューターはどんな方法でも実際に考えなければ判断できません。
チェスや将棋では予めチェスや将棋以外のことを考えないようにするためフレーム問題は生じませんが、いろいろな状況に対応する人工知能ではこの問題を無視できません。
こうして人工知能は当初の期待とは裏腹に現実の問題よりはるかに単純なパズル、迷路、チェスなどしか解けないことがわかりました。そして1970年代に入るとブームは急速に冷めていきました。
第二次人工知能ブーム
1980年代に入ると、ハードディスクなどコンピューターの外部記憶装置が進歩し、それまでよりはるかに大量のデータを扱えうことができるようになりました。そこで専門家（エキスパート）の知識をコンピューターに大量に入れたエキスパートシステムを使い、現実の複雑な問題をコンピューターで解くことが試みられました。
つまり第一次人工知能ブームの時のように論理学的アプローチで世界を完全に記述する汎用人工知能はとりあえずおいておいて、もっと限られた範囲で人間の知識をベースにコンピューターで問題を解決する取組でした。
医療現場での活用
スタンフォード大学では1970年代からエキスパートシステムに取り組み、エキスパートシステム「マイシン（Mycin）」は500ほどのルールでできた知識ベースを持ち、医師は質問に「はい/いいえ」で答えれば原因と思われる細菌のリストと推奨される抗生物質を示しました。
マイシンは正解率が65%で、細菌感染が専門でない医師よりはよい結果が出ました。しかし専門医の診断結果(80%)ほどではありませんでした。
現実世界の問題が解けるように見えたエキスパートシステムですが、そのためには専門家のあらゆる知識を教え込まなければならず、多数のルールを教えている間には互いに矛盾するルールも出てきました。
コンピューターは矛盾したルールにぶつかると止まってしまい、また教えていない事例に直面するとコンピューターは対処できませんでした。エキスパートシステムもルールが明確な簡単な事例にしか対処できず、複雑で例外も起こりうる現実世界には対処できませんでした。
こうして、今度こそはと思われた二回目のブームは深い失望とともに終結し、またしても人工知能は二回目の冬の時代に突入していきます。
世界トップを目指した日本の第五世代コンピューター
1980年代通産省は、産官学の最先端の研究者を集めて、欧米のコンピューターをしのぐ世界一斬新なコンピューターをつくるために、第五世代コンピューター開発プロジェクトを10年間500億円の予算で行いました。
これは「人間の言葉を理解し、人間とコミュニケートしながら問題解決するコンピューター」でつまり人工知能のことでした。
こうして出来上がった並列推論マシンは当時の技術では画期的なコンピューターでしたが「人間の言葉を理解し、人間とコミュニケートしながら問題解決」は実現できず、プロジェクトは失敗に終わりました。
強いAIと弱いAI
これは哲学者ジョン・サールが作った用語で、彼は強いAIは単なる道具ではなく、正しくプログラムされたコンピューターには精神が宿ると考えました。
【弱いAI】
人間の認知能力を必要としない問題解決や推論を行うコンピューターのことで、例としてディープ・ブルーのようなチェスプログラムがあります。弱いAIが意識を持ったり、人間並みの認知能力を示すことはないとされています。
【強いAI】
人間の知能に迫り人間の仕事をこなしたり、幅広い知識と何らかの意識を持つAIのことです。
【汎用人工知能（Artificial General Intelligence）】
汎用人工知能（AGI）は人間レベルの知能の実現を実現したAIのことです。
ここに至って、科学は人工知能を考えるうえで、今まで触れられなかった意識の問題を避けて通ることができなくなりました。
チューリングテストに合格すれば知能があると考えることに対して、哲学者のジョン・サールは以下の問いを投げかけました。
【中国語の部屋】
チューリングテストに合格したコンピューターは知能があるという考えに対して、哲学者ジョン・サールは1980年に発表した概念です。
英語しかわからない人が部屋にいて、その部屋には、中国語がわからなくても、中国語で書かれた問いかけに完全な回答ができる説明書がありました。すると部屋の人は英語しか分からなくても、中国語で書かれた質問の紙を見て、質問に適した中国語の回答を、説明書を見て中国語で書いて答えることができます。この場合、中国語で受け答えができるからといって中国語が分かるとは限りません。
同様に、チューリングテストに合格して知能があるような受け答えができたからといって、本当に知能があるかどうかは分からないという反論です。
こうして第二次人工知能ブームが終焉を迎えた後、2010年代に再び第三次人工知能ブームが訪れました。
では現在、知能とは何か？意識とは何か？
といった問題は解決したのでしょうか？
今使われている人工知能はどのような技術をもとにしているのでしょうか？
これについては、「人工知能AIの発達で仕事はどう変わるのか」 ～その2 第三次人口知能ブームの技術とシンギュラリティ～でお伝えします。
本コラムは2019年9月15日「未来戦略ワークショップ」のテキストから作成しました。
経営コラム ものづくりの未来と経営
人工知能、フィンテック、5G、技術の進歩は加速しています。また先進国の少子高齢化、格差の拡大と資源争奪など、私たちを取り巻く社会も変化しています。そのような中
ものづくりはどのように変わっていくのでしょうか？
未来の組織や経営は何が求められるのでしょうか？
経営コラム「ものづくりの未来と経営」は、こういった課題に対するヒントになるコラムです。
こちらにご登録いただきますと、更新情報のメルマガをお送りします。
（登録いただいたメールアドレスは、メルマガ以外には使用しませんので、ご安心ください。）
経営コラムのバックナンバーはこちらをご参照ください。
中小企業でもできる簡単な原価計算のやり方
製造原価、アワーレートを決算書から計算する独自の手法です。中小企業も簡単に個々の製品の原価が計算できます。以下の書籍、セミナーで紹介しています。
書籍「中小企業・小規模企業のための個別製造原価の手引書」
中小企業の現場の実務に沿ったわかりやすい個別製品の原価の手引書です。
基本的な計算方法を解説した【基礎編】と、自動化、外段取化の原価や見えない損失の計算など現場の課題を原価で解説した【実践編】があります。
中小企業・小規模企業のための
個別製造原価の手引書 【基礎編】
価格 ￥2,000 + 消費税(￥200）+送料
中小企業・小規模企業のための
個別製造原価の手引書 【実践編】
価格 ￥3,000 + 消費税(￥300）+送料
ご購入及び詳細はこちらをご参照願います。
書籍「中小製造業の『製造原価と見積価格への疑問』にすべて答えます！」日刊工業新聞社
普段疑問に思っている間接費・販管費やアワーレートなど原価と見積について、分かりやすく書きました。会計の知識がなくてもすらすら読める本です。原価管理や経理の方にもお勧めします。
こちら(アマゾン)から購入できます。
簡単、低価格の原価計算システム
数人の会社から使える個別原価計算システム「利益まっくす」
「この製品は、本当はいくらでできているだろうか？」
多くの経営者の疑問です。「利益まっくす」は中小企業が簡単に個別原価を計算できるて価格のシステムです。
設備・現場のアワーレートの違いが容易に計算できます。
間接部門や工場の間接費用も適切に分配されます。
クラウド型でインストール不要、1ライセンスで複数のPCで使えます。
利益まっくすは長年製造業をコンサルティングしてきた当社が製造業の収益改善のために開発したシステムです。
ご関心のある方はこちらからお願いします。詳しい資料を無料でお送りします。
